隨機變數 (Random Variables) 以及期望值 (Expectation) 是初學機率導論時兩個相當重要的觀念。制定隨機變數可以幫助我們更靈活地將機率實驗 (Random Experiment) 中欲關注的量進行連結。而期望值則代表了將所有可能出現的實驗結果，依照出現的機率進行加權平均之後的值。根據大數法則，只要實驗次數趨近無窮大，我們所關注的量在多次實驗中的總平均值就會趨近於期望值。

對我來說，初學隨機變數與期望值最精彩的一個例子，便屬優惠券蒐集問題 Coupon Collector's Problem 了。題目是這樣的：有一套 N 種優惠券，每一次抽獎都能均勻地隨機獲得 N 種之中的其中一種。請問要抽獎幾次才能湊齊一整套 N 種優惠券？

簡單的分析是這樣的：對所有介於 1 與 N 之間的正整數 k，我們定義 X_k 為『在獲得第 k-1 種不同的優惠券之後，抽了幾次獎才能夠獲得第 k 種不同的優惠券』，那麼不難算出 X_k 的期望值恰好是 N/(N-k+1)。利用期望值的可加性，我們得出湊滿一整套優惠券的期望抽獎次數剛好就是調和數 (Harmonic Numbers)：

它可以應用在各種地方：比如說，在玩寶可夢的時候，每一個區域出現的寶可夢有著不同的機率，你至少要偶遇幾次才可以遇到所有可能會出現的種類；又或者當年統一超商推出的 Hello Kitty 磁鐵蒐集活動 (請參考游森棚教授(教官)的文章)；各種 SSR 角色抽卡蒐集活動；又或者至少大樂透要開幾次獎才能夠讓所有數字至少出現過一次以上等等。

我們現在就來寫個簡單實驗來驗證一下吧。

from matplotlib import pyplot as plt
import numpy as np
from scipy.special import digamma
plt.style.use("seaborn-v0_8") # beautiful!

每一次模擬時所呼叫的函數：

def coupon_collecting(N):
    occur = [0] * N      # 紀錄每一種分別拿到幾次。
    count = 0            # 紀錄已獲得幾種。
    steps = 0            # 紀錄抽獎次數。
    while count < N:
        steps += 1
        i = np.random.randint(N) # 產生 0 到 N-1 之間的均勻隨機整數。
        occur[i] += 1
        count += (1 if occur[i] == 1 else 0)
        
    return steps

對於每一種優惠券的數量 N，我們進行 50 次實驗，並且紀錄其平均值。

max_N = 200
xs = np.array(range(1, max_N + 1))
ys = []
for N in xs:
    retry = 50
    data = [coupon_collecting(N) for _ in range(retry)]
    ys.append(np.mean(data))

# 跟答案做比較：我們繪製 n*Hn
hn = np.array([digamma(s+1) for s in xs]) + np.euler_gamma
zs = np.multiply(xs, hn)

將結果製圖～

import matplotlib.font_manager as font_manager
font = font_manager.FontProperties(family=['Arial', 'LiHei Pro'],
                                   style='normal', size=12)

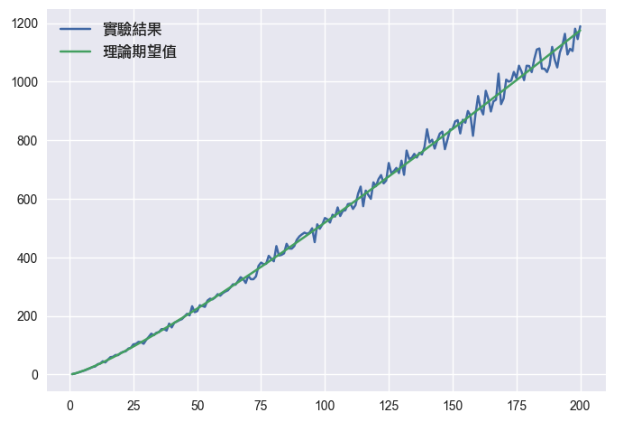
plt.plot(xs, ys, label='實驗結果')
plt.plot(xs, zs, label='理論期望值')
plt.legend(loc='upper left', prop=font)
plt.show()

兩條線看起來大致地吻合呢！

今天的爛梗：如果是馬可夫先生推出了優惠券，那我們就可以稱它為馬可夫券了。